Domain Decomposition Methodology for Solving Maxwell’s Equations
One basic research that we have conducted is the study of robust yet efficient ways for solving Maxwell Equations. The research, usually called computational electromagnetics (CEM), is highly mathematical and abstract in itself, and can be stated as one of the principal research topics in electromagnetic fields. The implication and impact of this research are astronomical. It is the heart of modern computer-aided engineering/computer-aided design (CAE/CAD) tools for advanced antennas, radio propagation, integrated circuits, EM interference and compatibility, signal and power integrity, and other applications in EM and microwave engineering.
Nowadays, ever-increasing fidelity and accuracy need for advanced EM applications have been pushing the problem sizes towards extreme scales. It puts a high premium on high-performance algorithms with optimal computational complexity. Moreover, increased demands are being placed on an integrated design and analysis environment, which requires new simulation tools to be well integrated into design processes. The goal of this research is to investigate first-principles modeling and analysis tools for these extremely large, multi-scale problems. The emphasis is placed on advancing parallel algorithms that are provably scalable, and facilitating a design-through-analysis paradigm for emerging and future complex systems.
In recent years, domain decomposition (DD) methods have enjoyed considerable success in solving large multi-scale EM problems. These methods feature divide-and-conquerin solution algorithms (applying the most suitable solution strategy to solve each sub-problem) and plug-in-play in software architectures (integrating individual EM solvers into a portable and extensible solution suite). They also result in highly efficient and naturally parallelizable algorithms on distributed memory many-core parallel computing systems.
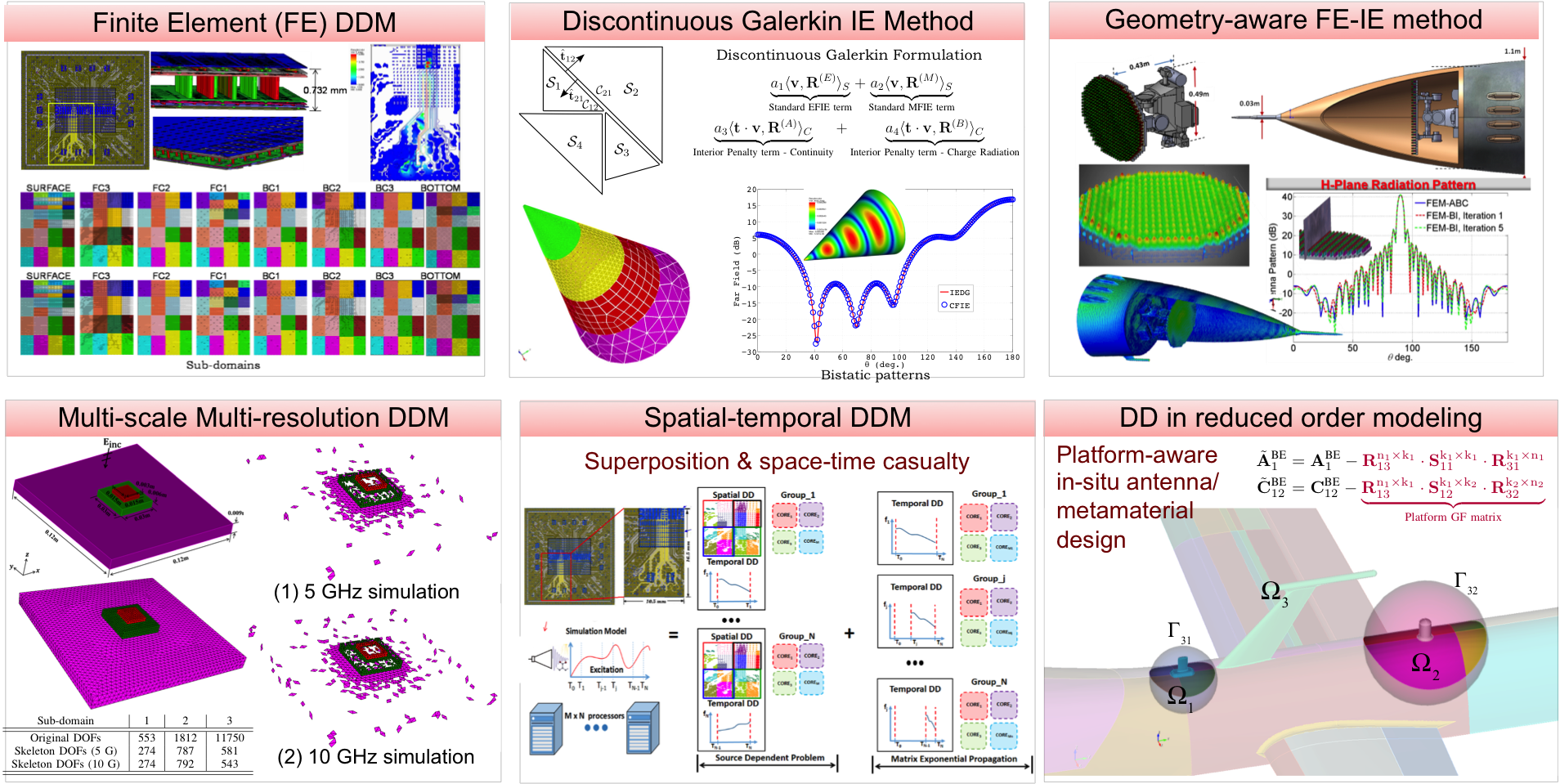
The main innovations in computational algorithms are summarized as follows:
Multi-resolution discontinuous Galerkin boundary element method (DG-BEM) [1–3].
The objective of this work is to allow the solution of integral equations using discontinuous trial and test functions without any consideration of continuity requirements across element’s boundaries. We can mix different types of elements and employ different order of basis functions within the same discretization. Built upon the DG-BEM, we investigate a rigorous, adaptive, and parallel coarse-graining method to reduce the computational complexity in the multi-scale computation. The work received 2014 IEEE Antenna and Propagation Sergei A. Schelkunoff Transactions Prize Paper Award.
[1] Z. Peng, K.-H. Lim, and J.-F. Lee, “A discontinuous Galerkin surface integral equation method for elec- tromagnetic wave scattering from nonpenetrable targets,” IEEE Trans. Antennas Propagat., vol. 61, no. 7, pp. 3617–3628, 2013.
[2] Z. Peng, R. Hiptmair, Y. Shao, and B. MacKie-Mason, “Domain decomposition preconditioning for surface integral equations in solving challenging electromagnetic scattering problems,” IEEE Trans. Antennas and Propagation, vol. 64, pp. 210–223, Jan 2016.
[3] H. Gao, Z. Peng, and X. Sheng, “A coarse-grained integral equation method for multiscale electromagnetic analysis,” IEEE Transactions on Antennas and Propagation, vol. 66, pp. 1607–1612, March 2018.
Geometry-aware domain decomposition method (GA-DDM) [4–6].
The work can be viewed as a problem decomposition, how to take a complex, multi-scale EM problem and divide it up into sub-problems that can be solved independently and concurrently. Research outcomes lead to: (1) divide-and-conquer in solution algorithms (applying the most suitable solution strategy to solve each sub-problem); (2) plug- in-play in software architectures (integrating individual EM solvers into a portable and extensible solution suite); (3) highly efficient and naturally parallelizable algorithms on distributed memory many-core parallel computing systems. The work received 2018 Best Transaction Paper Award - IEEE Transactions on Components, Packaging and Manufacturing Technology.
[4] V. Dolean, M. J. Gander, S. Lanteri, J.-F. Lee, and Z. Peng, “Effective transmission conditions for domain decomposition methods applied to the time-harmonic curl-curl Maxwell’s equations,” J. Comput. Phys., vol. 280, pp. 232–247, Jan. 2015.
[5] H. Gao, Z. Peng, and X. Q. Sheng, “A geometry-aware domain decomposition preconditioning for hybrid finite element-boundary integral method,” IEEE Transactions on Antennas and Propagation, vol. PP, no. 99, pp. 1–1, 2017.
[6] Z. Peng, Y. Shao, H. W. Gao, S. Wang, and S. Lin, “High-fidelity, high-performance computational algorithms for intrasystem electromagnetic interference analysis of IC and electronics,” IEEE Transactions on Components, Packaging and Manufacturing Technology, vol. PP, no. 99, pp. 1–16, 2017.
Space-time parallel computation for Maxwell’s Equations [7-8].
A recent breakthrough in my research is the parallel-in-time computation for time-dependent EM wave problems. The objective is to leverage the emerging exascale high-performance computing (HPC) platforms to address the space-scale and time-scale challenges in extreme fidelity EM analysis. (Best Student Paper Award in 2018 ACES conference, Best Conference Paper Award at 2019 EPEPS conference)
[7] Shu Wang, Yang Shao, and Zhen Peng, “A Parallel-in-Space-and-Time Method for Transient Electromagnetic Problems,” IEEE Trans. Antennas Propag., vol. 67, no. 6, pp. 3961-3973, June 2019.
[8] Shu Wang and Zhen Peng, “A Novel Space-Time Building Block Methodology for Transient Electromagnetic Analysis,” 28th Conference on Electrical Performance of Electronic Packaging and Systems, Montreal, Quebec, Canada, October 2019.
Multi-trace boundary integral equation method [9–11].
A novel multi-trace boundary IE formulation is investigated for the solution of the time-harmonic EM problems in large and deep cavities. The new formulation leads to a well-conditioned system equation, and it is immune from cavity resonances effects
[9] R. Hiptmair, C. Jerez-Hanckes, J.-F. Lee, and Z. Peng, “Domain decomposition for boundary integral equations via local multi-trace formulations,” in Domain Decomposition Methods in Science and Engineering XXI (J. Erhel, M. J. Gander, L. Halpern, G. Pichot, T. Sassi, and O. Widlund, eds.), vol. 98 of Lecture Notes in Computational Science and Engineering, pp. 43–57, Springer International Publishing, 2014.
[10] Z. Peng, K.-H. Lim, and J.-F. Lee, “A boundary integral equation domain decomposition method for electromagnetic scattering from large and deep cavities,” J. Comput. Phys., vol. 280, no. 1, pp. 626–642, 2015.
[11] Z. Peng, “A novel multitrace boundary integral equation formulation for electromagnetic cavity scattering problems,” IEEE Trans. Antennas Propagat., vol. 63, pp. 4446–4457, Oct 2015.
DDM for reduced order model [12–13].
The proposed work starts with a stationary-variable domain decomposition, where the computational domain is decomposed into large fixed parts and small portions with local variations. Subsequently, we introduce a separable and compressible platform Green’s function at the outer surface of those variable subdomains in an upfront offline calculation. Once obtained, the online computational complexity does not depend on the size of the in situ platform. (Best Student Paper Award in 2019 ACES conference)