Physics-Oriented Statistical Wave Analysis Integrating Order and Chaos

Collaborators: Thomas Antonsen@UMD, Steven Anlage@UMD, Zachary Drikas@NRL, Bisrat Addissie@NRL, Edl Schamiloglu@UNM, Sameer Hemmady@UNM

Even though we are seeking the highest possible fidelity, the computer representation will not be exactly the same compared to the real world. These uncertainties may arise from imprecise knowledge of the system, small differences in manufacturing, or numerical errors in the simulations. For integrable, regular wave systems, these small differences can be considered as local perturbations of the entire system. Hence, the numerical solution is still a very good approximation to the exact solution of the physical problem. However, the situation can be completely different in non-integrable, wave-chaotic systems. The EM wave solutions can be extremely sensitive to details and initial conditions. It makes the traditional first-principles deterministic approaches relevant only to a specific realization.

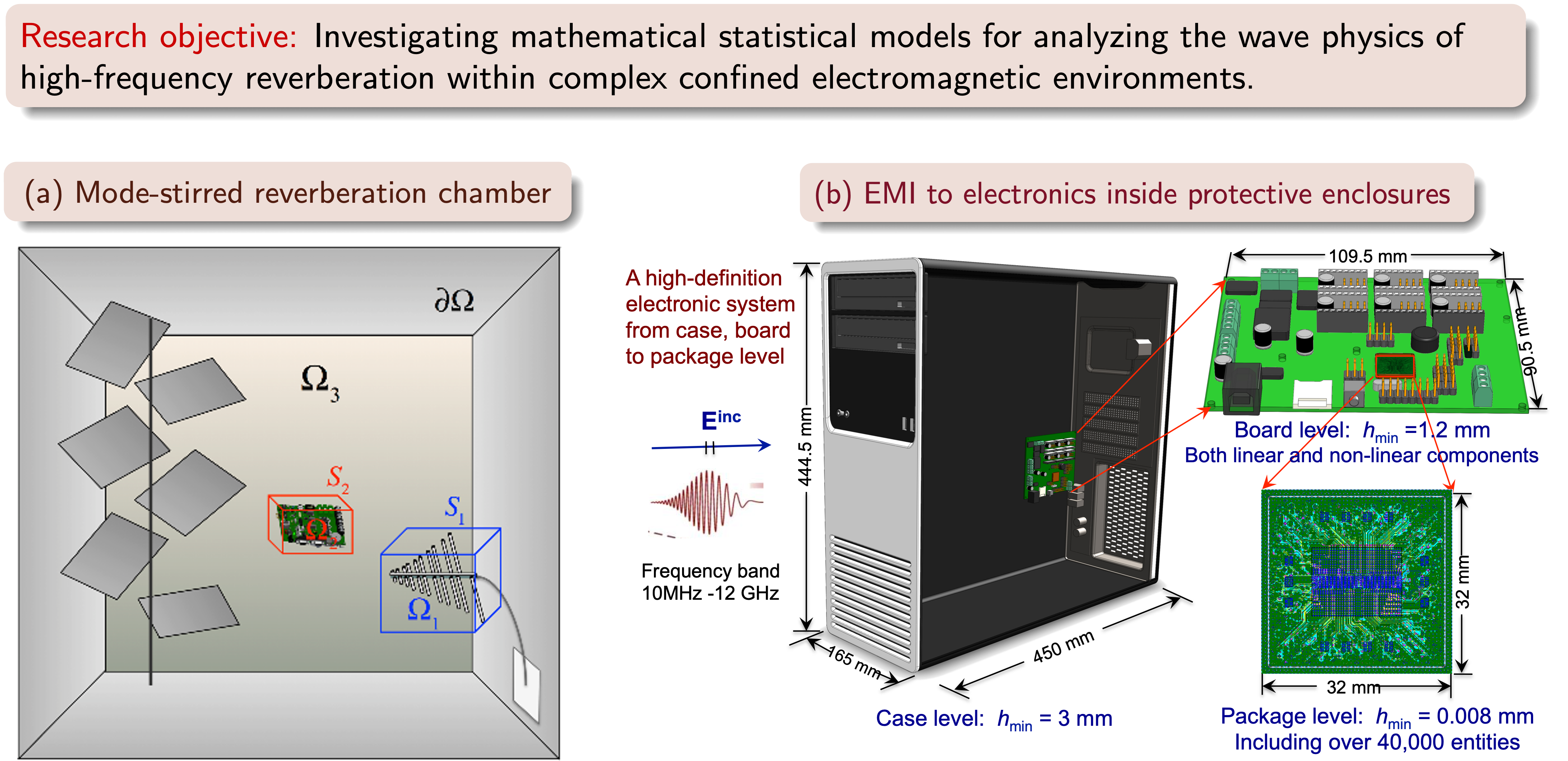
Wave chaos concerns solutions of wave equations, which in the semiclassical limit or short-wavelength limit can be described by chaotic ray trajectories. One representative class of wave-chaotic problems is confined EM systems, e.g. the antennas and electronics within large and complicated enclosures. In the high-frequency regime, the complex boundary of the enclosure can lead to high modal density and high modal overlap. Wave solutions inside these enclosures show strong fluctuations that are extremely sensitive to the exact geometry of the enclosure, the location of internal electronics, and the operating frequency. The extreme sensitivity and nonequilibrium nature make it a challenging task to analyze the uncertain behavior of the interactions. The fundamental difficulty of treating classically non-integrable systems has been precisely realized by the applied physics community. The chaotic dynamics have been discussed in the context of acoustics, electromagnetics, and quantum mechanics.

This project investigates an innovative theoretical solution to Maxwell’s Equations in the wave chaotic (random, diffusive) media. The fundamental solution, named stochastic Green’s function, rigorously integrates the coherent and incoherent contributions within a unified compact form. Furthermore, by incorporating the component-, site-, system-specific information with the universal chaotic dynamics, the work accomplishes a comprehensive framework for thestatistical analysis and uncertainty quantification of complex wave systems. The advancements will achieve first-ever an imperative simulation-driven, design-under-chaos capability, and a virtual experimental facility statisticallyreplicating real-world wave propagation environments. 

Along the line of research, we have advanced the theory of SGF from the spatial domain (narrowband) to broadband frequency domain and delay-Doppler domain. The work accomplishes a physics-oriented, mathematically tractable statistical wave model with diverse applications, including the mode-stirred reverberation chamber (2019 IEEE EMC Symposium Best Paper Award), EMC/EMI of electronic systems (2021 EPEPS Best Paper Award), information transmission in wave-chaotic indoor channels, statistical design of time-reversal systems, wavefront shaping and focusing, sensing and targeting.

Theory and Derivation of Scalar Stochastic Green’s Function

[1] S. Lin, Z. Peng, and T. Antonsen, “A Stochastic Green’s Function for Solution of Wave Propagation in Wave-Chaotic Environments,” IEEE Trans. Antennas Propag., vol. 68, no. 5, pp. 3919-3933, May 2020.

Theory and Derivation of Vector Dyadic Stochastic Green’s Function

[2] S. Lin, S. Luo, S. Ma, J. Feng, Y. Shao, Z. B. Drikas, B. D. Addissie, S. M. Anlage, T. Antonsen, and Z. Peng, “Predicting Statistical Wave Physics in Complex Enclosures: A Stochastic Dyadic Green’s Function Approach,” in IEEE Transactions on Electromagnetic Compatibility, vol. 65, no. 2, pp. 436-453, April 2023.

Investigation of the Space-time Stochastic Green’s Function

[3] S. Lin and Z. Peng, “On the Statistical Analysis of Space-Time Wave Physics in Complex Enclosures,” 30th Conference on Electrical Performance of Electronic Packaging and Systems, October 2021.

Investigation of the Broadband Stochastic Green’s Function

[4] S. Lin and Z. Peng, “Statistical Analysis of Information Transmission in Ray-Chaotic Enclosures: A Stochastic Green’s Function Approach”, 2020 IEEE International Symposium on Antennas and Propagation, July 2020.

https://resourcecenter.ieeeaps.org/conferences/2020-ap-symposium/APS2020SYM0060.html